O sistema binário é a base fundamental da computação e da eletrônica digital. Todos os dispositivos computacionais modernos utilizam esse sistema para representar e processar dados. Neste post, vamos explorar em detalhes o que é o sistema binário, como ele funciona, como converter entre diferentes bases numéricas e algumas curiosidades sobre sua aplicação.
O que é o Sistema Binário?
O sistema binário é um sistema de numeração posicional que utiliza apenas dois dígitos: 0 e 1. Cada posição em um número binário representa uma potência de 2, da mesma forma que no sistema decimal cada posição representa uma potência de 10.
Exemplo de Notação Posicional
No sistema decimal, escrevemos o número 321 assim:
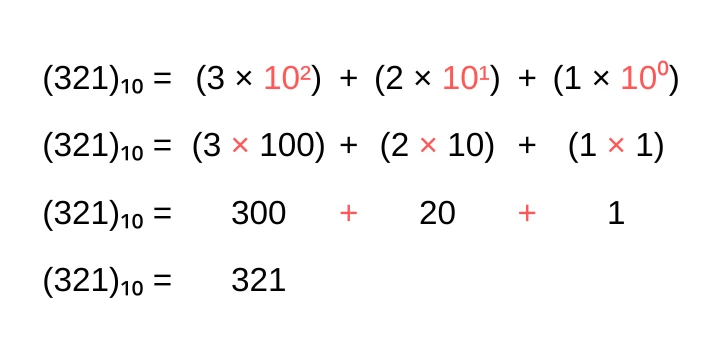
Agora que entendemos a notação posicional no sistema decimal, podemos expandir esse conceito para um sistema que utiliza apenas dois algarismos: o sistema binário.
Por que apenas 0 e 1?
O sistema binário é a base da computação porque os computadores trabalham com circuitos eletrônicos que só reconhecem dois estados distintos:
- Ligado (1) → Presença de energia elétrica
- Desligado (0) → Ausência de energia elétrica
Diferente dos humanos, que usam dez algarismos (0-9) porque historicamente contavam nos dedos, os computadores precisam de um sistema simples e confiável. Como os circuitos eletrônicos são feitos de transistores que podem estar ligados ou desligados, o binário se tornou a linguagem natural da computação.
A importância da energia no circuito
Saber se há ou não energia em um circuito é essencial para que o computador possa interpretar informações corretamente.
Cada bit armazenado na memória, processado pelo CPU ou transmitido na rede é, na verdade, um conjunto de sinais elétricos representando 0s e 1s.
Isso permite que o hardware entenda comandos, armazene informações e execute programas com extrema precisão.
Exemplo simples de funcionamento
Vamos imaginar um interruptor de luz em casa:
| Interruptor | Estado | Representação Binária |
|---|---|---|
| Desligado | Sem energia | 0 |
| Ligado | Com energia | 1 |
Se tivermos vários interruptores, podemos armazenar diferentes combinações de 0s e 1s, que formam números, letras e até imagens digitais!
Exemplo prático: Se tivermos 4 interruptores, cada um pode estar ligado (1) ou desligado (0), gerando combinações como:
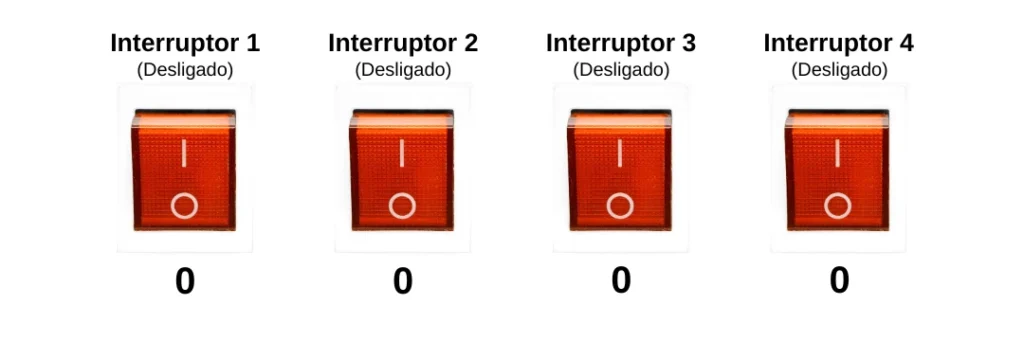
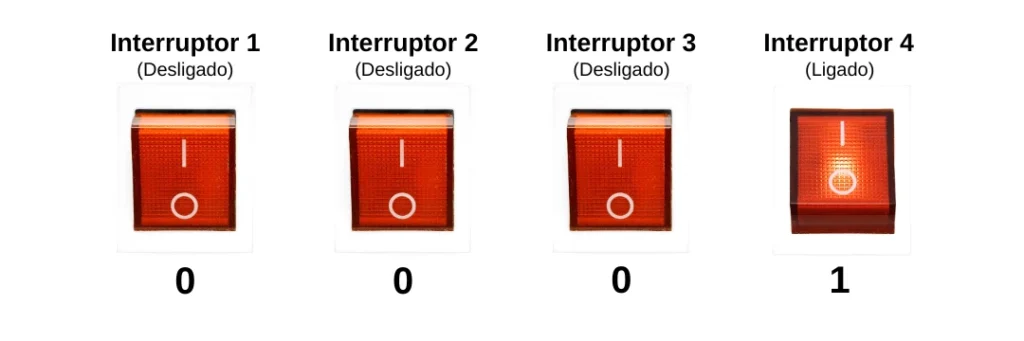



Esses padrões de bits são usados pelos computadores para representar números, armazenar dados e executar cálculos.
Armazenamento e Processamento dos Dados Binários
Agora que sabemos como os números binários podem ser formados através de combinações de 0s e 1s, precisamos entender como eles são armazenados e processados pelo computador. Afinal, quando olhamos para uma longa sequência de números binários, como:
01101010011011110110111001100001parece um monte de algarismos sem sentido, certo? 🤯
Mas será que o computador também vê dessa forma? A resposta é não!
Assim como usamos interruptores para representar números binários de forma visual, os computadores precisam de uma maneira eficiente de armazenar e interpretar esses bits.
É aí que entram os dispositivos de armazenamento, como as fitas magnéticas, os discos rígidos (HDDs) e os chips de memória (RAM, SSDs, etc.).
Fitas Magnéticas: Os Primeiros Discos Rígidos

Nos primórdios da computação, os dados eram armazenados em fitas magnéticas, onde cada bit (0 ou 1) era representado magneticamente.
O cabeçote de leitura passava pela fita e interpretava os bits como pulsos elétricos. Se houvesse magnetismo em uma área da fita, o computador lia como 1. Se não houvesse, lia como 0.
Como a fita magnética identificava os dados?
Ela utilizava padrões e marcadores para separar os números e instruções, garantindo que os bits fossem organizados corretamente.
Era como um texto codificado, onde o computador sabia exatamente onde começava e terminava cada conjunto de informações.
Esses marcadores serviam para indicar:
- O início e o fim de um conjunto de dados
- Separação entre diferentes registros ou arquivos
- Erros na gravação, permitindo correção automática
Exemplos de Marcadores Usados em Fitas Magnéticas
Marcador de Fim de Registro (End-of-Record, EOR)
Cada conjunto de dados armazenado na fita era chamado de registro. Para indicar onde um registro terminava, era inserido um byte especial como delimitador.
Exemplo prático:
Uma fita armazenando nomes de usuários poderia ter algo assim:
01001000 01100101 01101100 01101100 01101111 11111111 01010100 01100101 01110011 01110100
👆 Aqui, o byte 11111111 (FF em hexadecimal) pode ser o marcador de fim de registro, separando os nomes "Hello" e "Test".
Agora que entendemos como os números binários podem ser formados e armazenados, surge uma nova questão: como o computador interpreta essas sequências de 0s e 1s como letras, palavras e mensagens compreensíveis?
Afinal, quando digitamos um texto ou abrimos um arquivo, não vemos apenas um monte de números binários na tela.
Os computadores utilizam padrões específicos para representar caracteres, sendo um dos mais conhecidos o ASCII (American Standard Code for Information Interchange).
Esse sistema permite converter sequências de bits em letras, números e símbolos que usamos diariamente. Mas como essa conversão acontece?
Vamos explorar isso passo a passo!
Como traduzir o código binário para letras?
O código citado é uma sequência de bits que pode representar caracteres em um sistema de codificação como o ASCII.
Vamos entender os passos para realizar essa tradução!
Passo 1: Separar os Bits em Grupos de 8 algarismos
Cada caractere em ASCII é representado por 8 bits (1 byte). Vamos dividir sua sequência corretamente:
01001000 01100101 01101100 01101100 01101111 11111111 01010100 01100101 01110011 01110100
Passo 2: Converter Cada Byte para Decimal
Cada byte pode ser convertido para um número decimal usando a tabela ASCII.
| Binário | Decimal | Caractere ASCII |
|---|---|---|
| 01001000 | 72 | H |
| 01100101 | 101 | e |
| 01101100 | 108 | l |
| 01101100 | 108 | l |
| 01101111 | 111 | o |
| 11111111 | 255 | (Marcador EOR) |
| 01010100 | 84 | T |
| 01100101 | 101 | e |
| 01110011 | 115 | s |
| 01110100 | 116 | t |
Passo 3: Interpretar os Caracteres
Agora que temos os valores correspondentes na tabela ASCII, podemos montar a string:
Hello Test- “Hello” é claramente reconhecido.
- (255) não faz parte do conjunto ASCII padrão e pode ser um caractere especial, erro ou marcador.
- “Test” aparece normalmente após ele.
Mas como sabemos que um byte corresponde a um determinado número na base decimal?
Se cada sequência de 0s e 1s representa algo no computador, precisamos de um método para interpretar esses valores corretamente.
Quando falamos de texto, utilizamos tabelas como o ASCII, mas e quando lidamos com números diretamente?
Como o computador consegue transformar uma sequência como 01100101 em um valor decimal que possamos entender?
Agora que já sabemos como os bits podem representar caracteres, parece um ótimo momento para explorarmos a conversão de números binários para decimais.
Vamos entender como funciona essa transformação e como podemos converter qualquer número binário para um valor que reconhecemos no nosso sistema numérico do dia a dia!
Conversão de Números Binários para Decimais
A conversão de binário para decimal é essencial porque o sistema decimal é o que usamos no dia a dia, enquanto os computadores trabalham internamente apenas com binário.
Sempre que interagimos com um computador, seja digitando números em uma calculadora, salvando arquivos ou até mesmo vendo um relógio digital, há uma conversão acontecendo entre esses dois sistemas numéricos.
Vamos entender o processo de conversão!
Como Funciona a Conversão de Binário para Decimal?
O sistema decimal usa a base 10, o que significa que cada posição em um número representa uma potência de 10 (como foi ilustrado no início do post).
Já o sistema binário usa a base 2, o que significa que cada posição em um número binário representa uma potência de 2.
Passo 1: Entender a Notação Posicional
Cada bit em um número binário tem um peso específico, baseado em potências de 2. O bit mais à direita representa 2⁰, o próximo 2¹, e assim por diante, aumentando da direita para a esquerda.
Exemplo de um número binário de 8 bits:
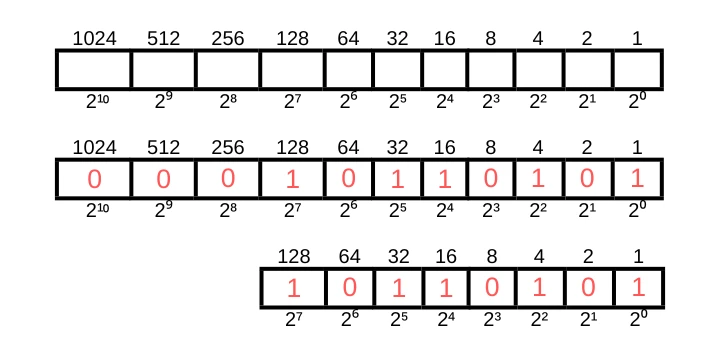
Cada bit pode ser 0 ou 1, e apenas os 1s são somados para obter o valor decimal, perceba que os zeros à esquerda foram desconsiderados por não influenciar.
Passo 2: Multiplicar Cada Bit pelo seu Peso
Vamos converter o número (10110101)₂ para decimal.
Primeiro, expandimos a equação:
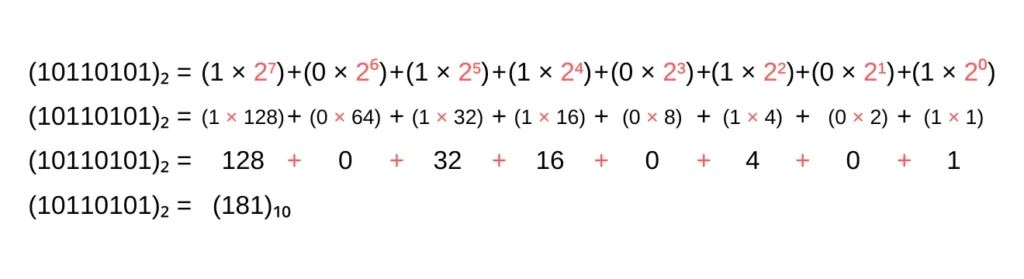
Por que essa Conversão é Tão Importante?
A conversão de binário para decimal é essencial porque nós, humanos, usamos a base 10, enquanto os computadores usam base 2.
Essa conversão permite que possamos:
- Interpretar dados armazenados no computador: Como valores numéricos em planilhas, contas bancárias e pontuações em jogos.
- Depurar e analisar códigos binários: Em programação, muitas vezes precisamos entender valores binários diretamente.
- Compreender endereços IP, cores RGB e outros formatos digitais: Muitos sistemas digitais usam valores binários que precisamos interpretar em decimal.
Cada vez que digitamos um número em uma calculadora digital, a máquina está convertendo nossa entrada decimal para binário, processando os cálculos e depois nos mostrando o resultado de volta em decimal!
Agora que sabemos converter binário para decimal, podemos explorar o processo inverso: como converter decimal para binário.
Conversão de Decimal para Binário
A conversão de decimal para binário é feita através de divisões sucessivas por 2, registrando os restos de cada divisão. O número binário final é obtido ao ler os restos de baixo para cima.
Vamos converter (11)₁₀ para binário:
Passo 1: Dividir por 2 e Registrar os Restos
| Divisão por 2 | Quociente | Resto |
|---|---|---|
| 11 ÷ 2 | 5 | 1 |
| 5 ÷ 2 | 2 | 1 |
| 2 ÷ 2 | 1 | 0 |
| 1 ÷ 2 | 0 | 1 |
Passo 2: Ler os Restos de Baixo para Cima
Agora, organizamos os restos na ordem inversa, formando o número binário:
(11)₁₀ = (1011)₂Portanto, 11 na base decimal é representado como 1011 na base binária.
Se precisar fazer o cálculo no papel, vou ilustrar na próxima imagem como ficaria o desenvolvimento:
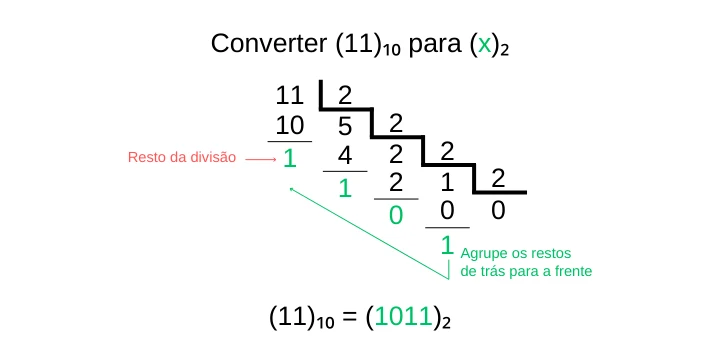
E agora que já sabemos como fazer a conversão de bases binárias para a base decimal, vamos tirar a prova real, para garantir que o cálculo foi feito corretamente.

Agora que dominamos as conversões entre decimal e binário, conseguimos representar qualquer número nesses dois sistemas. Aprendemos que os computadores trabalham internamente apenas com 0s e 1s, mas também vimos que números binários podem se tornar longos e difíceis de interpretar para humanos.
Por exemplo, representar o número 365 em binário resulta em (101101101)₂, o que pode ser complicado de ler e manipular rapidamente. Se já temos o sistema decimal (que usamos no dia a dia) e o binário (essencial para os computadores), surge uma questão:
Por que precisamos de mais duas bases numéricas: octal (base 8) e hexadecimal (base 16)?
A resposta está na necessidade de uma representação mais compacta e legível para grandes quantidades de bits.
Em vez de trabalhar com sequências enormes de 0s e 1s, podemos utilizar sistemas intermediários que facilitam a conversão e interpretação de números binários.
Sistema Octal (Base 8)
- Usa apenas os dígitos 0 a 7.
- Cada grupo de 3 bits binários pode ser representado por um único dígito octal.
Sistema Hexadecimal (Base 16)
- Usa os dígitos 0 a 9 e as letras A a F (onde A = 10, B = 11, C = 12, D = 13, E = 14, F = 15).
- Cada grupo de 4 bits binários pode ser representado por um único dígito hexadecimal.
Essas bases foram introduzidas para facilitar a leitura e a escrita de números binários, especialmente na programação e na arquitetura de computadores.
Em breve, vou trazer novos posts falando sobre como converter binário para octal e hexadecimal e entenderemos por que essas representações são tão úteis no mundo digital.
Espero ter ajudado até aqui, obrigado pela leitura!

